Thống kê là gì? Kiến thức tổng quan nhất về thống kê

IQ, EQ và SQ: Ba yếu tố trí tuệ bạn cần để thành công
15 November, 2024
KPI đánh giá kết quả công việc trong doanh nghiệp logistics
18 November, 2024Last updated on 11 August, 2025
“Thống kê (Statistics)” – một khái niệm quen thuộc nhưng không phải ai cũng thực sự hiểu rõ về vai trò và ứng dụng của nó trong cuộc sống. Từ việc phân tích số liệu kinh doanh, dự đoán xu hướng thị trường đến hỗ trợ các nghiên cứu khoa học, thống kê hiện diện trong mọi lĩnh vực và là chìa khóa để đưa ra các quyết định chính xác, dựa trên dữ liệu.
Trong bài viết dưới đây, OCD sẽ cùng bạn khám phá khái niệm “Thống kê là gì?” và cung cấp những kiến thức tổng quan nhất về lĩnh vực đầy thú vị này.
Thống kê (Statistics) là gì?

Khái niệm thống kê
Thống kê (Statistics) là một nhánh của toán học ứng dụng liên quan đến việc thu thập, mô tả, phân tích và suy diễn kết luận từ những dữ liệu định lượng. Các lý thuyết toán học đằng sau thống kê thường là pháp tính vi phân và tích phân, đại số tuyến tính, lý thuyết xác suất.
Những người làm công việc thống kê được gọi là nhà thống kê học (statisticians). Công việc của họ là xác định cách thức đưa ra các kết luận đáng tin cậy về các nhóm lớn (tổng thể) hoặc các sự kiện chung dựa trên hành vi và đặc điểm quan sát được từ các mẫu nhỏ. Những mẫu nhỏ này được coi như đại diện cho một phần của nhóm lớn hơn.
Bản chất của thống kê
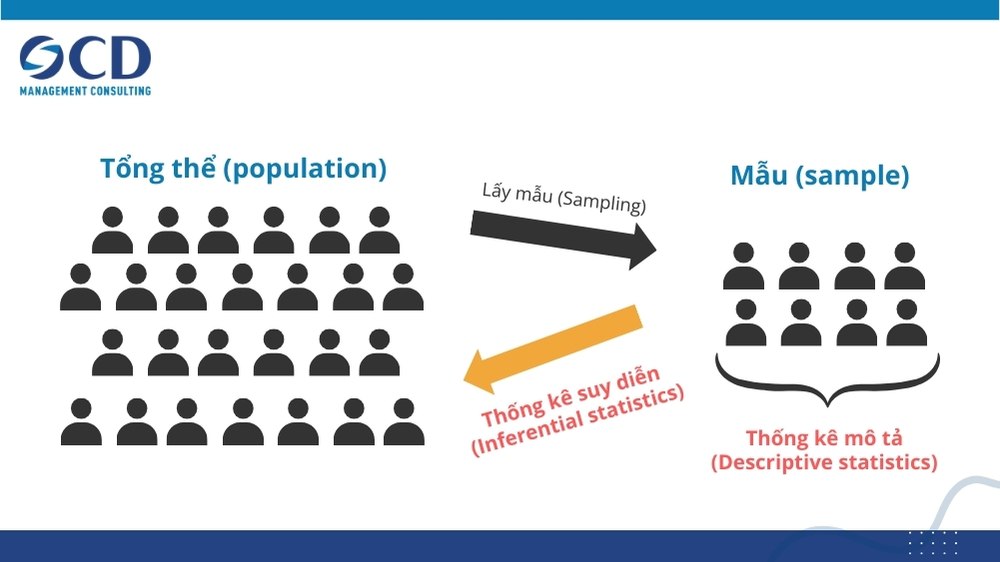
Trong thực tế, thống kê được phát triển dựa trên ý tưởng rằng chúng ta có thể tìm hiểu các đặc tính của một tập hợp lớn các đối tượng hoặc sự kiện (“tổng thể thống kê” hay “population”) bằng cách nghiên cứu các đặc điểm của một số ít các đối tượng hoặc sự kiện trong tổng thể đó (“mẫu” hay “sample”). Việc thu thập dữ liệu đầy đủ về toàn bộ tổng thể thường quá tốn kém, khó khăn, hoặc không khả thi, vì vậy thống kê bắt đầu từ nghiên cứu một mẫu có thể quan sát được một cách tiện lợi hoặc tiết kiệm.
Các nhà thống kê đo lường và thu thập dữ liệu về các cá nhân hoặc phần tử trong một mẫu, sau đó phân tích dữ liệu này để tạo ra các thống kê mô tả (descriptive statistics). Từ các đặc điểm quan sát được của dữ liệu mẫu, họ có thể suy luận hoặc đưa ra dự đoán có căn cứ về các đặc tính chưa được đo lường của tổng thể rộng hơn. Đây được gọi là thống kê suy diễn (inferential statistics).
Thống kê mô tả là gì?
Thống kê mô tả (Descriptive Statistics) là một nhánh của thống kê tập trung vào việc tóm tắt và trình bày dữ liệu sao cho dễ hiểu và dễ phân tích. Nó không rút ra kết luận hay dự đoán, mà chỉ cung cấp một cái nhìn tổng quan, trực diện nhất về tập dữ liệu.
Các công cụ chính của thống kê mô tả:
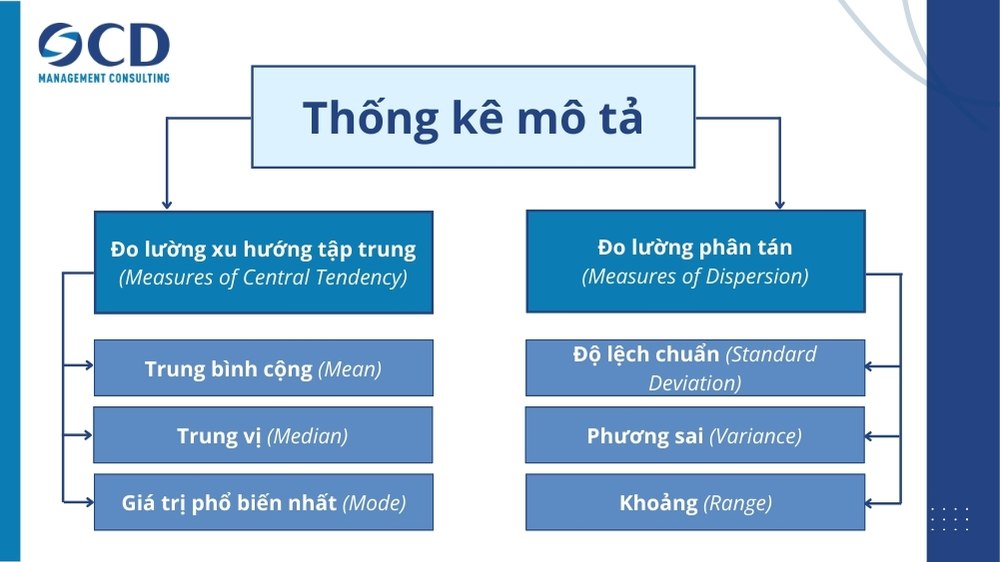
Thống kê mô tả (Descriptive Statistics)
- Đo lường xu hướng tập trung (Measures of Central Tendency):
- Trung bình cộng (Mean)
- Trung vị (Median)
- Giá trị phổ biến nhất (Mode)
- Đo lường phân tán (Measures of Dispersion):
- Độ lệch chuẩn (Standard Deviation)
- Phương sai (Variance)
- Khoảng (Range)
- Biểu đồ và bảng biểu:
- Biểu đồ cột, biểu đồ tròn, biểu đồ hộp, biểu đồ histogram.
- Bảng phân bố tần số
Thống kê mô tả không chỉ giúp mô tả sự khác biệt giữa các đặc điểm quan sát được của từng phần tử (element) mà còn giúp hiểu rõ hơn các thuộc tính chung của tập dữ liệu mẫu. Đây cũng là cơ sở để kiểm định giả thuyết và đưa ra dự đoán thông qua thống kê suy diễn.
Thống kê suy diễn là gì?
Thống kê suy diễn (Inferential Statistics) tập trung vào việc rút ra kết luận hoặc đưa ra dự đoán về tổng thể (population) dựa trên dữ liệu từ một mẫu dữ liệu (sample).
Mục tiêu chính của thống kê suy diễn:
- Ước lượng (Estimation):
- Sử dụng dữ liệu mẫu để dự đoán tham số của tổng thể, như giá trị trung bình của tổng thể hoặc tỷ lệ tổng thể.
- Ví dụ: Ước lượng điểm trung bình của toàn bộ sinh viên trong trường dựa trên dữ liệu mẫu của 100 sinh viên.
- Kiểm định giả thuyết (Hypothesis Testing):
- Kiểm tra xem một giả thuyết về tổng thể có đúng hay không.
- Ví dụ: Xác định xem một loại thuốc có hiệu quả hơn loại thuốc khác hay không.
- Dự đoán (Prediction):
- Dự đoán kết quả tương lai dựa trên dữ liệu hiện có.
- Ví dụ: Dự đoán doanh số bán hàng của một công ty trong năm tới dựa trên dữ liệu từ các năm trước.
Bảng so sánh
| Tiêu chí | Thống kê mô tả | Thống kê suy diễn |
| Mục tiêu | Tóm tắt và trình bày dữ liệu | Rút ra kết luận về tổng thể hoặc đưa ra dự báo |
| Phạm vi dữ liệu | Làm việc với dữ liệu đã có | Suy luận từ mẫu đến tổng thể |
| Kết quả | Mô tả đặc điểm dữ liệu | Dự đoán hoặc kiểm định giả thuyết |
| Ví dụ | Tính độ tuổi trung bình của một xã | Dự đoán độ tuổi trung bình của cả huyện hoặc cả tỉnh |
Cả hai loại thống kê đều đóng vai trò quan trọng và thường bổ trợ lẫn nhau trong nghiên cứu và phân tích dữ liệu.
Dữ liệu thống kê
Dữ liệu thống kê là tập hợp các thông tin thu thập được từ các hiện tượng, sự vật hoặc quá trình mà chúng ta quan tâm. Những thông tin này có thể là số liệu, từ ngữ, hoặc các đặc tính khác, được thu thập, ghi chép và phân tích để rút ra những kết luận nhất định. Dữ liệu thống kê có thể được phân loại theo nhiều cách khác nhau, nhưng hai cách phân loại phổ biến nhất là:
Phân loại dựa trên tính chất
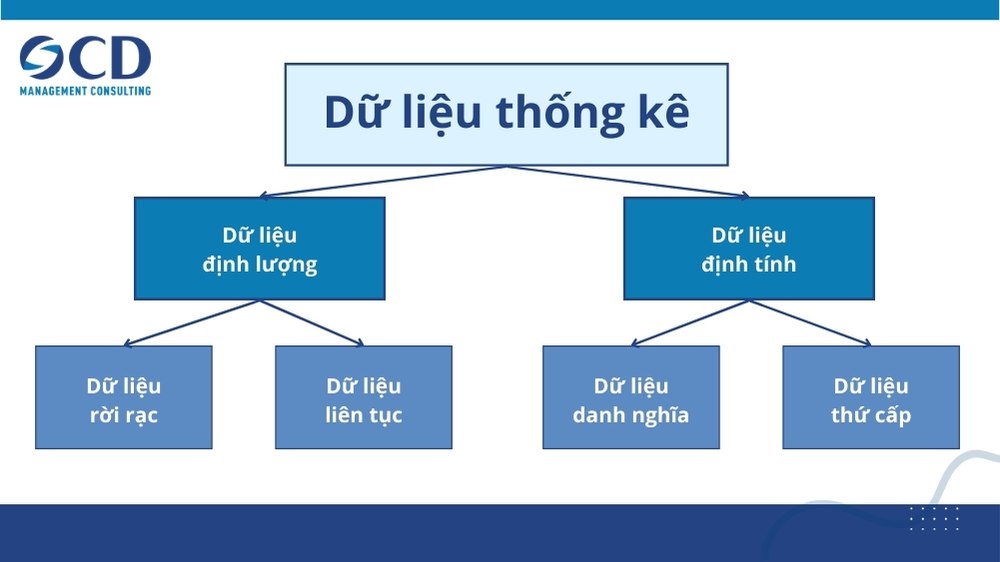
Dữ liệu thống kê được phân loại dựa trên tính chất
- Dữ liệu định lượng (Quantitative): Là những dữ liệu thể hiện số lượng hoặc mức độ của một hiện tượng.
- Dữ liệu rời rạc (Discrete): Chỉ nhận những giá trị nguyên (ví dụ: số lượng học sinh trong lớp, số lượng xe ô tô).
- Dữ liệu liên tục (Continuous): Có thể nhận bất kỳ giá trị nào trong một khoảng nhất định (ví dụ: chiều cao, cân nặng, nhiệt độ).
- Dữ liệu định tính (Qualitative): Là những dữ liệu mô tả các đặc tính, thuộc tính của một đối tượng.
- Dữ liệu danh nghĩa (Nominal): Dùng để phân loại các đối tượng vào các nhóm khác nhau (ví dụ: giới tính, màu sắc, quốc tịch).
- Dữ liệu thứ bậc (Ordinal): Dùng để sắp xếp các đối tượng theo một thứ tự nhất định (ví dụ: xếp loại học lực, mức độ hài lòng).
Phân loại dựa trên nguồn gốc
- Dữ liệu sơ cấp: Là dữ liệu được thu thập trực tiếp từ nguồn gốc, thông qua các phương pháp như khảo sát, phỏng vấn, quan sát. Ví dụ: Kết quả khảo sát ý kiến của sinh viên về chất lượng giảng dạy
- Dữ liệu thứ cấp: Là dữ liệu đã được thu thập và xử lý bởi các tổ chức khác, được công bố trên các báo cáo, tạp chí, hoặc các nguồn thông tin khác. Ví dụ: số liệu thống kê về dân số của một tỉnh (lấy từ báo cáo của Tổng cục Thống kê).
Các loại thang đo trong thống kê
Có 4 loại thang đo chính trong thống kê, sau khi phân tích các biến và kết quả. Mỗi loại thang đo có cách định lượng kết quả theo những cách khác nhau.
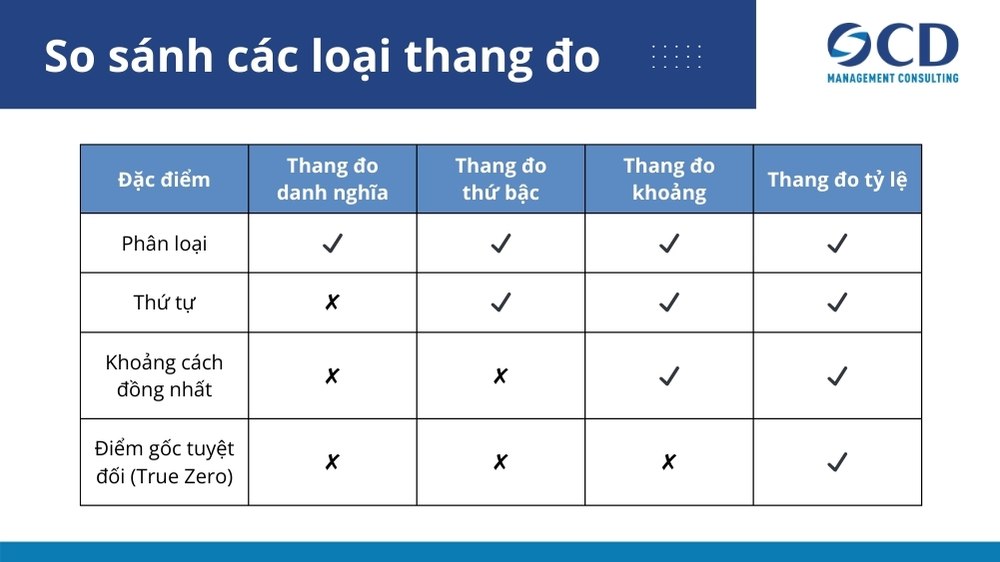
Bảng so sánh các loại thang đo
Thang đo danh nghĩa (Nominal scale)
Thang đo danh nghĩa hay thang đo định danh (Nominal Scale) là một loại thang đo cơ bản trong thống kê, dùng để phân loại hoặc gán nhãn cho các đối tượng, nhóm, hoặc biến mà không có giá trị số học hoặc sắp xếp theo thứ tự cụ thể. Nó chỉ nhằm mục đích xác định sự khác biệt giữa các nhóm hoặc phần tử, chứ không thể hiện bất kỳ mối quan hệ định lượng hay thứ bậc nào.
Ví dụ:
- Giới tính: Nam, Nữ.
- Nhóm máu: A, B, AB, O.
- Quốc tịch: Việt Nam, Nhật Bản, Hoa Kỳ.
- Màu sắc yêu thích: Đỏ, Xanh, Vàng, Trắng.
Trong trường hợp thang đo là danh nghĩa, bạn có thể sử dụng biến giả để gán giá trị số học cho nó. Ví dụ, để tiện thu thập dữ liệu và chuẩn bị nhập liệu vào cơ sở dữ liệu máy tính, chúng ta có thể dùng biến giả cho biến Giới tính, trong đó:
- 0 biểu thị người đó là nam
- 1 biểu thị người đó là nữ
Thang đo thứ bậc (Ordinal scale)
Thang đo thứ bậc (Ordinal Scale) được sử dụng để sắp xếp hoặc phân loại các đối tượng, nhóm, hoặc biến theo một thứ tự nhất định, nhưng không đo lường được khoảng cách giữa các thứ hạng. Nó thể hiện mối quan hệ “cao hơn” hoặc “thấp hơn” giữa các danh mục, nhưng không cho biết cụ thể khoảng cách hoặc mức độ chênh lệch giữa chúng.
Ví dụ:
- Xếp hạng chất lượng dịch vụ: Tốt, Khá, Trung bình, Kém.
- Mức độ hài lòng: Rất hài lòng, Hài lòng, Không hài lòng.
- Xếp hạng cuộc thi: Hạng Nhất, Hạng Nhì, Hạng Ba.
- Trình độ học vấn: Tiểu học, Trung học, Đại học, Sau đại học.
Thang đo khoảng (Interval scale)
Thang đo khoảng (Interval Scale) dùng để sắp xếp các giá trị theo thứ tự và đo lường khoảng cách giữa các giá trị một cách có ý nghĩa. Tuy nhiên, thang đo này không có điểm gốc bằng 0 mang tính tuyệt đối, nên các phép tính tỷ lệ (như gấp đôi, gấp ba) không có ý nghĩa.
Ví dụ về nhiệt độ:
- Các mức nhiệt độ: 10°C, 20°C, 30°C.
- Khoảng cách giữa 10°C và 20°C (10 độ) bằng khoảng cách giữa 20°C và 30°C (10 độ).
- Giải thích: Điểm 0°C không có nghĩa là “không có nhiệt độ” mà chỉ là một điểm quy ước. Vì vậy, không thể nói 30°C “nóng gấp ba lần” 10°C.
Ví dụ trong dịch vụ khách hàng:
- Khách hàng được yêu cầu đánh giá mức độ hài lòng của họ đối với dịch vụ trên thang điểm từ 1 đến 10.
- 1: Hoàn toàn không hài lòng.
- 10: Hoàn toàn hài lòng.
- Giải thích: Khoảng cách giữa các điểm (ví dụ: từ 4 lên 5 hoặc từ 7 lên 8) là như nhau, nhưng “0 điểm” không tồn tại trong thang đo vì nó không mang ý nghĩa “không hài lòng”. Hơn nữa, cũng không thể nói khách hàng cho 10 điểm (hoàn toàn hài lòng) sẽ hài lòng “gấp 10 lần” khách hàng cho 1 điểm (hoàn toàn không hài lòng).
Thang đo tỷ lệ (Ratio scale)
Thang đo tỷ lệ (Ratio Scale) là mức thang đo cao nhất trong các loại thang đo, có đầy đủ các đặc điểm của thang đo khoảng (Interval Scale) nhưng khác biệt ở chỗ nó có điểm gốc tuyệt đối (true zero). Điểm gốc này biểu thị sự vắng mặt hoàn toàn của đặc tính được đo lường, cho phép thực hiện các phép tính tỷ lệ (nhân, chia).
Ví dụ:
- Chiều dài và chiều cao:
- Một cây cao 0m có nghĩa là không tồn tại chiều cao.
- Một cây cao 2m gấp đôi chiều cao của cây cao 1m.
- Khối lượng:
- Một vật nặng 0 kg nghĩa là không có khối lượng.
- Một vật nặng 10kg gấp đôi khối lượng của vật nặng 5kg
Các phương pháp lấy mẫu trong thống kê
Trong thống kê, phương pháp lấy mẫu là cách thức chọn ra một nhóm đại diện (mẫu) từ tổng thể (dân số) để thực hiện nghiên cứu, nhằm đưa ra những kết luận cho toàn bộ tổng thể. Dưới đây là một số phương pháp lấy mẫu phổ biến:
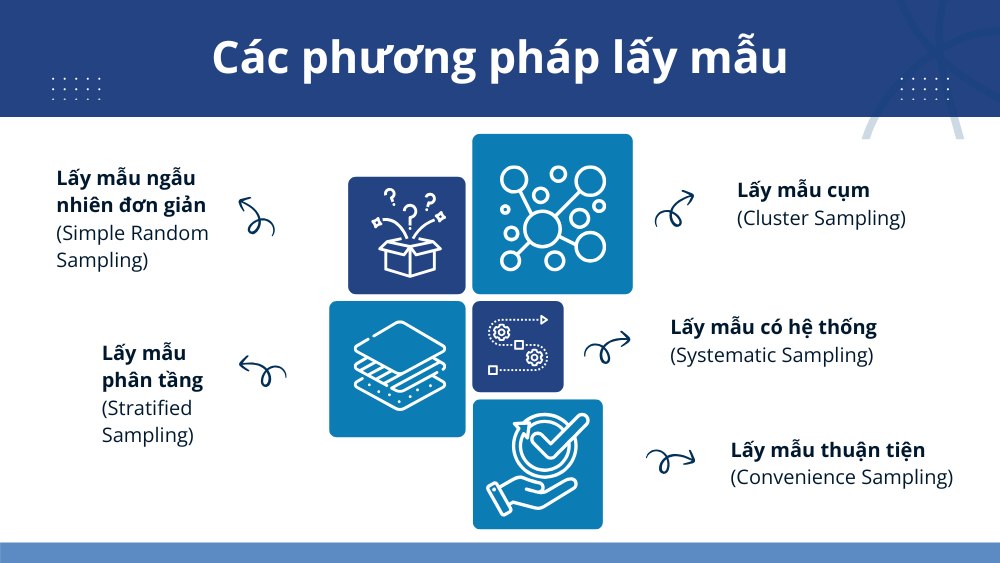
Các phương pháp lấy mẫu trong thống kê
Lấy mẫu ngẫu nhiên đơn giản (Simple Random Sampling)
- Đặc điểm: Mỗi cá thể trong tổng thể có một cơ hội, xác suất bằng nhau để được chọn vào mẫu.
- Cách thực hiện: Lấy ngẫu nhiên bằng cách sử dụng máy tính, hoặc chọn thủ công ngẫu nhiên.
- Ưu điểm: Đảm bảo tính công bằng, dễ thực hiện.
- Nhược điểm: Cần danh sách đầy đủ các phần tử trong tổng thể, có thể không thuận tiện khi tổng thể lớn.
Ví dụ: Chọn ngẫu nhiên 100 sinh viên từ tổng thể 1000 sinh viên trong trường đại học để khảo sát.
Lấy mẫu phân tầng (Stratified Sampling)
- Đặc điểm: Tổng thể được chia thành các nhóm (tầng) khác nhau, rồi mẫu được lấy ngẫu nhiên từ mỗi tầng.
- Cách thực hiện: Chia tổng thể thành các tầng (ví dụ: theo độ tuổi, giới tính, khu vực), sau đó lấy mẫu ngẫu nhiên từ mỗi tầng.
- Ưu điểm: Cải thiện tính đại diện của mẫu, giảm sai số.
- Nhược điểm: Cần phân loại chính xác các tầng, và đôi khi có thể phức tạp trong việc xác định các tầng.
Ví dụ: Trong nghiên cứu thị trường, chia người tham gia thành các nhóm tuổi (18-24, 25-34, 35-44,…) lấy mẫu ngẫu nhiên từ mỗi nhóm tuổi.
Lấy mẫu cụm (Cluster Sampling)
- Đặc điểm: Tổng thể được chia thành các cụm nhỏ (nhóm con), sau đó một hoặc vài cụm được chọn ngẫu nhiên để khảo sát.
- Cách thực hiện: Chia tổng thể thành các nhóm, rồi chọn một số nhóm để lấy mẫu. Tất cả các phần tử trong các nhóm đã chọn sẽ được đưa vào mẫu.
- Ưu điểm: Tiết kiệm chi phí và thời gian, dễ thực hiện khi tổng thể lớn và phân tán.
- Nhược điểm: Mẫu có thể không đại diện đầy đủ nếu các cụm không đồng đều.
Ví dụ: Chọn ngẫu nhiên một số trường học (cụm) trong một thành phố, sau đó khảo sát toàn bộ học sinh trong các trường đó.
Lấy mẫu có hệ thống (Systematic Sampling)
- Đặc điểm: Chọn mẫu theo một quy luật nhất định từ một danh sách được sắp xếp sẵn.
- Cách thực hiện: Chọn một điểm bắt đầu ngẫu nhiên, sau đó chọn các phần tử theo khoảng cách cố định.
- Ưu điểm: Dễ thực hiện và tiết kiệm thời gian.
- Nhược điểm: Nếu có sự thay đổi theo chu kỳ trong tổng thể, kết quả có thể không chính xác.
Ví dụ: nếu có 100 cá thể được xếp thành hàng và đánh số, và điểm bắt đầu ngẫu nhiên là cá thể thứ 5, thì mỗi cá thể thứ 10 tiếp theo (ví dụ: 5, 15, 25,…) sẽ được chọn cho đến khi có 10 mẫu được chọn.
Lấy mẫu thuận tiện (Convenience Sampling)
- Đặc điểm: Lấy mẫu từ những phần tử dễ tiếp cận nhất trong tổng thể.
- Cách thực hiện: Chọn những cá thể mà bạn dễ tiếp cận hoặc có sẵn.
- Ưu điểm: Tiết kiệm thời gian, chi phí.
- Nhược điểm: Không đảm bảo tính đại diện, dễ dẫn đến sai lệch trong kết quả.
Ví dụ: Phỏng vấn những người đang mua sắm tại một trung tâm thương mại để khảo sát.
Ứng dụng thống kê trong thực tế
Thống kê là một công cụ mạnh mẽ được ứng dụng rộng rãi trong nhiều lĩnh vực thực tế. Dưới đây là một số ứng dụng tiêu biểu:
Kinh doanh và Marketing
- Phân tích thị trường: Thống kê giúp hiểu nhu cầu khách hàng, xu hướng mua sắm và hành vi tiêu dùng để xây dựng chiến lược kinh doanh.
- Hiệu quả chiến dịch marketing: Đánh giá mức độ thành công của các chiến dịch quảng cáo dựa trên số liệu như tỷ lệ chuyển đổi, mức độ tương tác và doanh số.
- Dự đoán doanh thu: Dựa trên dữ liệu lịch sử để dự báo doanh thu trong tương lai.
Y tế và Sức khỏe
- Nghiên cứu y học: Phân tích dữ liệu thử nghiệm lâm sàng để đánh giá hiệu quả của thuốc hoặc liệu pháp điều trị.
- Dịch tễ học: Theo dõi và dự đoán sự bùng phát dịch bệnh, ví dụ như COVID-19.
- Quản lý bệnh viện: Tối ưu hóa sử dụng giường bệnh, nhân sự và tài nguyên y tế dựa trên dữ liệu.
Giáo dục
- Đánh giá chất lượng giảng dạy: Sử dụng thống kê để đo lường hiệu quả của các phương pháp dạy học.
- Theo dõi kết quả học tập: Phân tích điểm số để xác định xu hướng, từ đó hỗ trợ cá nhân hóa quá trình học tập cho học sinh.
Công nghiệp và Sản xuất
- Kiểm soát chất lượng: Thống kê giúp phát hiện lỗi và đảm bảo sản phẩm đạt tiêu chuẩn trong quy trình sản xuất.
- Tối ưu hóa quy trình: Phân tích dữ liệu để cải thiện hiệu suất, giảm lãng phí và tiết kiệm chi phí.
Tài chính và Đầu tư
- Quản lý rủi ro: Sử dụng các mô hình thống kê để đánh giá và giảm thiểu rủi ro trong đầu tư.
- Dự đoán thị trường tài chính: Phân tích dữ liệu lịch sử để dự đoán giá cổ phiếu hoặc xu hướng thị trường.
Công nghệ và AI
- Học máy (Machine Learning): Dựa trên dữ liệu thống kê để huấn luyện các mô hình dự đoán và ra quyết định.
- Phân tích dữ liệu lớn: Tìm kiếm xu hướng và mối quan hệ trong dữ liệu lớn để hỗ trợ ra quyết định chiến lược.
Quản lý nhà nước
- Điều tra dân số: Thống kê giúp thu thập và phân tích dữ liệu dân số để hoạch định chính sách.
- Quản lý giao thông: Dự đoán lưu lượng giao thông, giảm ùn tắc và tối ưu hóa quy hoạch đô thị.
Các bước cơ bản để sử dụng phần mềm SPSS cho thống kê
Để sử dụng phần mềm SPSS (Statistical Package for the Social Sciences) để tiến hành các phân tích thống kê, bạn có thể làm theo các bước cơ bản dưới đây. SPSS là một phần mềm mạnh mẽ dùng để phân tích và xử lý dữ liệu trong nhiều lĩnh vực, từ nghiên cứu khoa học đến nghiên cứu thị trường.
Giao diện phần mềm SPSS
Bước 1: Chuẩn bị dữ liệu
Cách thực hiện như sau:
- Thu thập dữ liệu: Đảm bảo rằng dữ liệu được thu thập đầy đủ và đúng định dạng.
- Xác định các biến: Biến định tính, biến định lượng, biến phụ thuộc, và biến độc lập.
- Làm sạch dữ liệu: Loại bỏ giá trị thiếu (missing values), kiểm tra và xử lý các giá trị ngoại lệ (outliers).
- Chuẩn bị file dữ liệu: Dữ liệu thường được lưu ở định dạng Excel (.xls, .xlsx), CSV hoặc nhập trực tiếp vào phần mềm SPSS.
Bước 2: Nhập dữ liệu vào phần mềm SPSS
- Mở SPSS: Chọn File → Open → Data để mở tệp dữ liệu hoặc nhập trực tiếp.
- Nhập dữ liệu thủ công:
- Chuyển sang tab Variable View để khai báo tên biến, kiểu dữ liệu (numeric, string), giá trị missing, và nhãn biến.
- Chuyển sang tab Data View để nhập dữ liệu từng dòng.
- Chuyển đổi dữ liệu từ Excel hoặc CSV:
- Import file bằng cách vào File → Open → Data.
- Chọn định dạng và thực hiện các bước định nghĩa biến nếu cần.
Bước 3: Tiến hành phân tích thống kê mô tả
Thống kê mô tả cơ bản:
- Vào Analyze → Descriptive Statistics → Frequencies (tần suất) hoặc Descriptives (giá trị trung bình, giá trị lớn nhất, nhỏ nhất, độ lệch chuẩn,…).
Vẽ biểu đồ:
- Dùng Graphs → Chart Builder để vẽ biểu đồ cột, histogram, hoặc biểu đồ tròn.
Bước 4: Thực hiện các suy diễn thống kê
- Kiểm tra giả thuyết: Thực hiện các bài kiểm định thống kê (t-test, ANOVA, chi-square…).
- Vào Analyze → Compare Means để so sánh trung bình.
- Vào Analyze → Nonparametric Tests để thực hiện kiểm định phi tham số.
- Phân tích hồi quy: Vào Analyze → Regression để xây dựng mô hình hồi quy.
- Kiểm tra độ tin cậy: Sử dụng Cronbach’s Alpha qua Analyze → Scale → Reliability Analysis.
Bước 5: Xem kết quả và phân tích
Kết quả sẽ xuất hiện trong cửa sổ Output. Bạn có thể phân tích và giải thích kết quả thống kê theo các chỉ số như:
- Mean (Trung bình)
- Standard Deviation (Độ lệch chuẩn)
- P-value (Giá trị p trong các phép kiểm định)
- Chi-squared value (Giá trị chi-squared)
Bước 7: Lưu và xuất kết quả
Bạn có thể lưu dữ liệu và kết quả phân tích dưới dạng tệp SPSS hoặc xuất ra các định dạng khác như Excel hoặc PDF:
- Lưu dữ liệu: Vào File > Save hoặc Save As để lưu tệp dữ liệu.
- Xuất kết quả: Vào File > Export để xuất kết quả ra các định dạng khác.
Kết luận
Thống kê là việc phân tích dữ liệu và rút ra kết luận từ kết quả mẫu. Trong nhiều doanh nghiệp từ các cơ quan chính phủ đến các định chế tài chính, thống kê được sử dụng để đưa ra kết luận về một vấn đề nào đó dựa trên một bộ dữ liệu nhất định.
Học thống kê có thể dẫn dắt bạn trở thành một nhà thống kê, nhưng nó cũng có thể là một công cụ hữu ích trong cuộc sống hàng ngày. Khi bạn có thể sử dụng nó để đánh giá khả năng sinh lời của một khoản đầu tư, hoặc xác định liệu bạn có bị tính giá quá cao so với chất lượng thực sự của sản phẩm hoặc dịch vụ hay không, thống kê có thể được sử dụng để có cái nhìn sâu sắc về các kết quả có thể xảy ra của các đối tượng hoặc sự kiện.
——————————-




