Thống kê mô tả là gì? Các loại thống kê mô tả phổ biến

Marketing Mix là gì? 4P, 7P và 4C
22 November, 2024
Khả năng chịu áp lực trong công việc: Làm sao để duy trì sự bình tĩnh khi đối mặt với deadline?
22 November, 2024Last updated on 21 July, 2025
Nhiều chuyên gia sử dụng thống kê mô tả (descriptive statistics) để trực quan hóa một bộ dữ liệu lớn, cung cấp cái nhìn sâu sắc về các đặc điểm chung của bộ dữ liệu và giúp các doanh nghiệp và tổ chức đưa ra quyết định sáng suốt. Khác với thống kê suy diễn, thống kê mô tả không đưa ra những lập luận. Thay vào đó, nó cung cấp cho bạn một nền tảng hiểu biết vững chắc về bộ dữ liệu mà bạn đang nghiên cứu. Cùng OCD tìm hiểu thêm về loại thống kê này trong bài viết dưới đây nhé!
Thống kê mô tả (Descriptive statistics) là gì?

Thống kê mô tả (Descriptive statistics) là một nhánh của thống kê liên quan đến việc tóm tắt, sắp xếp và trình bày dữ liệu một cách ý nghĩa và ngắn gọn. Nó tập trung vào việc mô tả và phân tích các đặc điểm chính của tập dữ liệu mà không đưa ra bất kỳ suy diễn hay kết luận nào cho tổng thể lớn hơn.
Mục tiêu chính của phương pháp thống kê mô tả là cung cấp một bản tóm tắt rõ ràng và ngắn gọn về bộ dữ liệu, giúp các nhà nghiên cứu hoặc nhà phân tích hiểu được các xu hướng và sự phân bố trong tập dữ liệu. Bản tóm tắt này thường bao gồm:
- Các đại lượng đo lường xu hướng tập trung (ví dụ: giá trị trung bình, trung vị, yếu vị).
- Các đại lượng đo lường độ phân tán (ví dụ: khoảng biến thiên, phương sai, độ lệch chuẩn).
- Hình dạng của phân phối (ví dụ: độ nhọn, độ lệch)
Thống kê mô tả cũng bao gồm việc trình bày dữ liệu dưới dạng đồ họa thông qua biểu đồ, đồ thị và bảng, giúp việc hình dung và diễn giải thông tin trở nên dễ dàng hơn. Các biểu đồ phổ biến bao gồm biểu đồ tần suất (histogram), biểu đồ cột, biểu đồ tròn, biểu đồ phân tán (scatter diagram) và biểu đồ hộp.
Bằng cách sử dụng thống kê mô tả, các nhà nghiên cứu có thể tóm tắt và truyền tải hiệu quả các đặc điểm chính của tập dữ liệu, từ đó hỗ trợ hiểu rõ hơn về dữ liệu và tạo nền tảng cho các phân tích thống kê chuyên sâu hoặc quá trình ra quyết định tiếp theo.
Tại sao phương pháp thống kê mô tả lại quan trọng?
Mặc dù phương pháp thống kê mô tả tương đối đơn giản về mặt toán học, nhưng chúng đóng một vai trò rất quan trọng trong bất kỳ dự án nghiên cứu nào. Thường thì, chúng ta hay bỏ qua phần thống kê mô tả và muốn nhanh chóng chuyển sang những phân tích thống kê suy diễn – một mảng có vẻ “thú vị” hơn. Tuy nhiên, điều này có thể là một sai lầm tốn kém.
Lý do là vì phương pháp thống kê mô tả giúp bạn, với vai trò là nhà nghiên cứu, hiểu rõ các đặc điểm chính của mẫu mà không bị lạc lối trong khối lượng dữ liệu thô khổng lồ. Nó cung cấp nền tảng cho phân tích định lượng sau này. Ngoài ra, thống kê mô tả còn cho phép bạn nhanh chóng nhận ra các vấn đề tiềm ẩn trong tập dữ liệu – ví dụ như các giá trị ngoại lệ (outliers) bất thường, dữ liệu bị thiếu,…
Quan trọng không kém, phương pháp thống kê mô tả còn giúp định hướng quá trình ra quyết định khi chọn phương pháp thống kê suy diễn, vì mỗi kiểm định suy diễn đều có yêu cầu cụ thể liên quan đến hình dạng phân phối dữ liệu.
Tóm lại, việc dành thời gian tìm hiểu kỹ phương pháp thống kê mô tả trước khi chuyển sang các phương pháp “nâng cao” hơn là điều cần thiết. Tùy thuộc vào mục tiêu và câu hỏi nghiên cứu của bạn, loại thống kê này có thể đóng vai trò then chốt trong nhiều trường hợp.
Các loại thống kê mô tả phổ biến
Phân phối tần suất
Phân phối tần suất là một cách biểu diễn dữ liệu để chỉ ra số lần xuất hiện của các giá trị hoặc kết quả trong một bộ dữ liệu. Nó mô tả tần suất (số lần) các giá trị xuất hiện trong một khoảng nhất định, một phạm vi giá trị hoặc một nhóm cụ thể. Phân phối tần suất có thể được trình bày dưới dạng bảng hoặc đồ thị.
Phân phối tần suất giúp nhóm các giá trị dữ liệu thành các lớp (hoặc nhóm) và đếm số lần mỗi lớp xảy ra. Điều này giúp dễ dàng nhận thấy các mẫu, xu hướng hoặc sự phân bố của dữ liệu, từ đó cung cấp cái nhìn sâu sắc về bộ dữ liệu đó.
Ví dụ, giả sử bạn tiến hành một cuộc khảo sát trong quận Thanh Xuân với 100 người tham gia để tìm hiểu về số giờ làm việc mỗi tuần của họ. Sau khi thu thập dữ liệu, bạn có thể tổ chức và phân tích kết quả dưới dạng phân phối tần suất như sau:
| Số giờ làm việc mỗi tuần | Tần suất (Số người) | Tỷ lệ phần trăm (%) |
| 0 – 10 giờ | 10 | 10% |
| 11 – 20 giờ | 20 | 20% |
| 21 – 30 giờ | 30 | 30% |
| 31 – 40 giờ | 25 | 25% |
| 41 – 50 giờ | 10 | 10% |
| Trên 50 giờ | 5 | 5% |
Đại lượng đo lường xu hướng tập trung
Đại lượng đo lường xu hướng tập trung (Measures of central tendency) là các số liệu thống kê mô tả có giá trị đại diện cho toàn bộ tập dữ liệu. Nói cách khác, chúng cho biết “điểm trung tâm” tập của dữ liệu.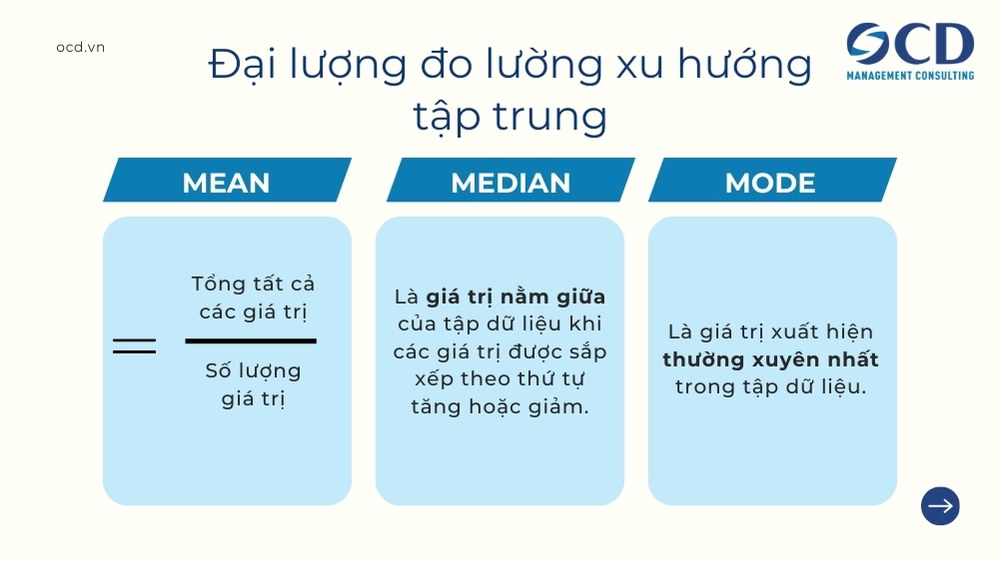
Ví dụ: Khi chúng ta nói đến điểm trung bình của một lớp học, chúng ta đang sử dụng một thước đo xu hướng tập trung để mô tả thành tích học tập chung của cả lớp.
Các đại lượng đo lường xu hướng tập trung phổ biến
Mean (Trung bình):
- Là giá trị trung bình cộng của tất cả các điểm dữ liệu trong tập dữ liệu.
- Công thức: Mean = Tổng tất cả các giá trị / Số lượng giá trị
- Ví dụ: Trong tập dữ liệu {1;5;6;8} thì Mean = (1+5+6+8)/4 = 5
- Ưu điểm: Phản ánh toàn bộ dữ liệu.
- Nhược điểm: Dễ bị ảnh hưởng bởi các giá trị ngoại lệ.
Median (Trung vị):
- Là giá trị nằm giữa của tập dữ liệu khi các giá trị được sắp xếp theo thứ tự tăng hoặc giảm.
- Nếu số lượng giá trị là lẻ, trung vị là giá trị chính giữa. Nếu là chẵn, trung vị là trung bình của hai giá trị ở giữa.
- Ví dụ:
- Tập {3;7;9;10;20} thì Median = 9
- Tập {1;2;2;6;7;12;21;51} thì Median = (6+7)/2 = 6,5
- Ưu điểm: Không bị ảnh hưởng bởi các giá trị ngoại lệ.
- Nhược điểm: Không sử dụng toàn bộ dữ liệu trong tính toán.
Mode (Yếu vị):
- Là giá trị xuất hiện thường xuyên nhất trong tập dữ liệu.
- Một tập dữ liệu có thể có một yếu vị, nhiều yếu vị hoặc không có yếu vị.
- Ví dụ:
- Tập {1,2,2,3,4,5,7,10}: Mode = 2
- Tập {1,1,2,2,3,4,6,8,9}: Modes = 1 và 2
- Ưu điểm: Dễ hiểu, đặc biệt hữu ích với dữ liệu dạng phân loại (categorical data)
- Nhược điểm: Không phải lúc nào cũng tồn tại hoặc là duy nhất.
Đại lượng đo lường độ phân tán
Measures of Dispersion (Các đại lượng đo lường độ phân tán) là những giá trị thống kê mô tả dùng để đo lường mức độ phân tán, biến động hoặc độ chênh lệch giữa các giá trị trong một tập dữ liệu. Chúng giúp đánh giá mức độ mà dữ liệu phân bố xung quanh một giá trị trung tâm như mean (giá trị trung bình cộng), và cung cấp cái nhìn sâu hơn về cấu trúc của tập dữ liệu.
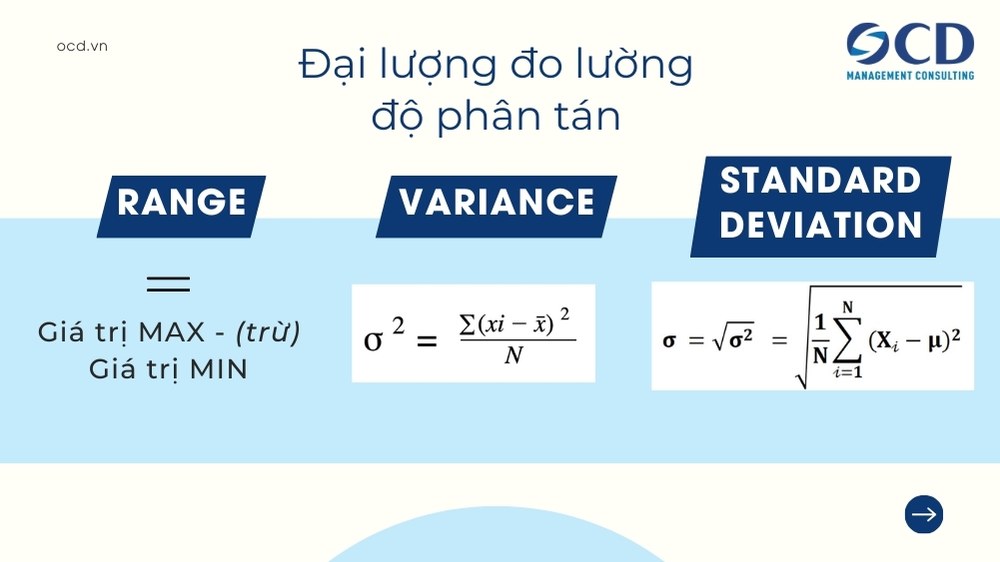
Các đại lượng đo lường độ phân tán phổ biến
Range (Khoảng biến thiên):
- Là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất trong tập dữ liệu.
- Công thức: Range = Giá trị lớn nhất – Giá trị nhỏ nhất
- Ví dụ: Trong tập {5,10,15,20} thì Range = 20 − 5 = 15
- Ưu điểm: Đơn giản, dễ tính.
- Nhược điểm: Không phản ánh đầy đủ mức độ phân tán nếu dữ liệu có giá trị ngoại lệ.
Variance (Phương sai):
- Là trung bình cộng của bình phương khoảng cách từ mỗi giá trị đến trung bình cộng (mean) của tập dữ liệu.
- Công thức: Variance= {∑[xi− Mean(x)]^2}/N (Với tập dữ liệu là tổng thể)
- Ví dụ: Tập {3,5,7}, Mean = 5, Variance = [(3−5)^2+(5−5)^2+(7−5)^2]/3=8/3
- Ưu điểm: Phản ánh sự biến động toàn diện.
- Nhược điểm: Đơn vị đo không giống với dữ liệu gốc (do có bình phương).
Standard Deviation (Độ lệch chuẩn):
- Là căn bậc hai của phương sai, thể hiện mức độ phân tán của dữ liệu so với trung bình.
- Công thức: Standard Deviation= √{Variance}
- Ví dụ: Nếu Variance = 8/3 thì Standard Deviation = √{8/3} = 1,633
- Ưu điểm: Đơn vị đo giống với dữ liệu gốc, dễ diễn giải.
Ưu điểm của thống kê mô tả
Một số lợi ích phổ biến mà bạn có thể nhận thấy khi sử dụng phương pháp thống kê mô tả bao gồm:
- Trình bày đơn giản: tất cả mọi người có nền tảng chuyên môn khác nhau có thể dễ dàng hiểu và áp dụng thống kê mô tả.
- Tóm tắt hiệu quả: Thống kê mô tả cho phép bạn chuyển hóa bộ dữ liệu phức tạp thành một vài con số đặc trưng, cô đọng để cung cấp cái nhìn tổng quan nhanh chóng.
- Biểu diễn đồ họa: Phương pháp thống kê mô tả có thể được trực quan hóa dễ dàng bằng các biểu đồ, đồ thị đa dạng, phong phú tùy thuộc vào nhu cầu riêng của mình.
Nhược điểm của thống kê mô tả
Về mặt hạn chế, hãy ghi nhớ những bất lợi sau:
- Báo cáo không có khả năng dự báo: Thống kê mô tả chỉ diễn giải những gì đã xảy ra. Nó không cung cấp cái nhìn sâu sắc hơn về lý do tại sao mọi việc lại xảy ra hoặc ý nghĩa của chúng đối với tương lai. Nói cách khác, bạn không thể đưa ra suy luận của mình về kết quả cho các nhóm đối tượng khác trong tổng thể hoặc rút ra kết luận từ giả thuyết.
- Khả năng hiểu sai: Phương pháp thống kê mô tả rất hữu ích trong việc nêu các đặc điểm nổi bật trong bộ dữ liệu của bạn, nhưng bạn phải cẩn thận trong việc lựa chọn bảng dữ liệu, biểu đồ thích hợp để cung cấp thông tin rõ ràng, chính xác và có đủ bối cảnh. Điều này giúp người xem có thể hiểu đúng thông tin mà không gây nhầm lẫn.
Những sự thật thú vị về phương pháp thống kê mô tả
Thống kê mô tả không chỉ là công cụ để tóm tắt dữ liệu mà còn ẩn chứa nhiều sự thật thú vị và bất ngờ. Dưới đây là một số điểm thú vị về lĩnh vực này:
Nền tảng cho mọi phân tích dữ liệu
- Phương pháp thống kê mô tả là bước đầu tiên trong mọi phân tích dữ liệu. Trước khi đào sâu vào các mô hình phức tạp hoặc dự đoán, thống kê mô tả giúp hiểu rõ bản chất của dữ liệu, như phân bố, xu hướng, và biến động.
- Mặc dù đơn giản, nó là công cụ không thể thiếu trong lĩnh vực Data Science, Machine Learning, và các ngành nghiên cứu khác.
Lịch sử lâu đời
- Thống kê mô tả có nguồn gốc từ những nền văn minh cổ đại. Ví dụ:
- Người Ai Cập đã sử dụng phương pháp thống kê mô tả để theo dõi dân số và nông nghiệp từ khoảng 3.000 năm TCN.
- Đế chế La Mã ghi chép chi tiết số liệu về dân số, tài nguyên, và quân đội để quản lý đế chế rộng lớn của mình.
Tính trung bình cộng dễ gây hiểu nhầm
- Trung bình cộng (mean) thường được sử dụng để đại diện cho dữ liệu, nhưng đôi khi nó không phản ánh đúng bản chất dữ liệu:
- Ví dụ kinh điển: tỷ phú Jeff Bezos bước vào một quán cà phê, và trung bình thu nhập của mọi người trong quán lập tức tăng lên mức hàng tỷ USD, dù bản chất đa số những người khác vẫn nghèo.
- Đây là lý do tại sao các thước đo khác như trung vị (median), mode hay độ lệch chuẩn cũng rất quan trọng.
Ứng dụng đa dạng trong cuộc sống
- Dữ liệu thống kê mô tả xuất hiện ở khắp nơi, từ kết quả bầu cử, xếp hạng âm nhạc, đến thống kê thể thao. Ví dụ:
- Trong bóng đá, chỉ số như tỷ lệ kiểm soát bóng, số cú sút trúng đích là những thống kê mô tả quan trọng giúp đánh giá hiệu suất của đội bóng.
Dữ liệu có thể “nói dối”
- Thống kê mô tả có thể bị bóp méo để dẫn đến những kết luận sai lệch nếu người dùng cố ý chọn số liệu một cách thiên vị. Ví dụ:
- Một công ty có thể chỉ báo cáo mức lương trung bình thay vì trung vị, để che giấu mức lương thấp của phần lớn nhân viên.
- Điều này nhấn mạnh vai trò của đạo đức trong phân tích dữ liệu.
Khám phá sự bất đối xứng của dữ liệu
- Phương pháp thống kê mô tả không chỉ đo lường trung tâm (mean, median) mà còn đo lường độ lệch (skewness) và độ nhọn (kurtosis), giúp chúng ta hiểu rõ hơn về hình dạng phân phối của dữ liệu.
- Ví dụ: Một phân phối thu nhập thường lệch phải vì phần lớn thu nhập tập trung ở mức thấp hoặc trung bình, trong khi một số ít người có mức thu nhập rất cao.
“Luật số lớn” trong thực tế
- Theo thống kê mô tả, nếu thu thập đủ dữ liệu, chúng ta có thể xác định các mẫu chung đáng tin cậy hơn.
- Điều này giải thích tại sao các cuộc khảo sát lớn như bầu cử thường có độ chính xác cao hơn, dù chỉ khảo sát một phần nhỏ dân số.
Sức mạnh của trực quan hóa dữ liệu
- Các biểu đồ như histogram, boxplot, hoặc scatter plot không chỉ làm dữ liệu dễ hiểu mà còn giúp nhận diện các mẫu hoặc điểm bất thường mà các con số thuần túy không thể hiện được.
- Một hình ảnh trực quan có thể truyền đạt ý nghĩa nhanh chóng hơn nhiều so với việc liệt kê các con số khô khan.
Phân phối chuẩn (Normal Distribution): Một kỳ quan tự nhiên
- Phân phối chuẩn xuất hiện ở khắp nơi trong tự nhiên và xã hội, từ chiều cao của con người đến điểm thi hoặc thậm chí các lỗi trong sản xuất. Điều thú vị là hầu hết các hiện tượng phức tạp đều có xu hướng hội tụ về một dạng phân phối chuẩn.
Sự khác biệt giữa trung bình và trung vị trong kinh tế
- Trong phân phối thu nhập hoặc tài sản, trung vị (median) thường là con số thực tế hơn trung bình.
- Ví dụ: Thu nhập trung bình toàn cầu là khoảng 10.000 USD/năm, nhưng thu nhập trung vị thực tế chỉ là 2.000-3.000 USD/năm do sự bất đối xứng và khoảng cách giàu nghèo.
Kết luận
Thống kê mô tả đóng vai trò quan trọng trong việc tóm tắt và trình bày dữ liệu một cách rõ ràng và dễ hiểu. Bằng cách sử dụng các công cụ như bảng, biểu đồ và các đại lượng đo lường, thống kê mô tả giúp chúng ta hiểu được các đặc điểm cơ bản của dữ liệu, từ đó đưa ra những nhận định và quyết định hợp lý.
Tuy nhiên, người sử dụng cần chú ý đến cách thức trình bày để tránh những hiểu lầm và đảm bảo tính chính xác trong việc diễn giải kết quả.
——————————-




